Spike Sorting by Clustering

Spike Sorting by Clustering#

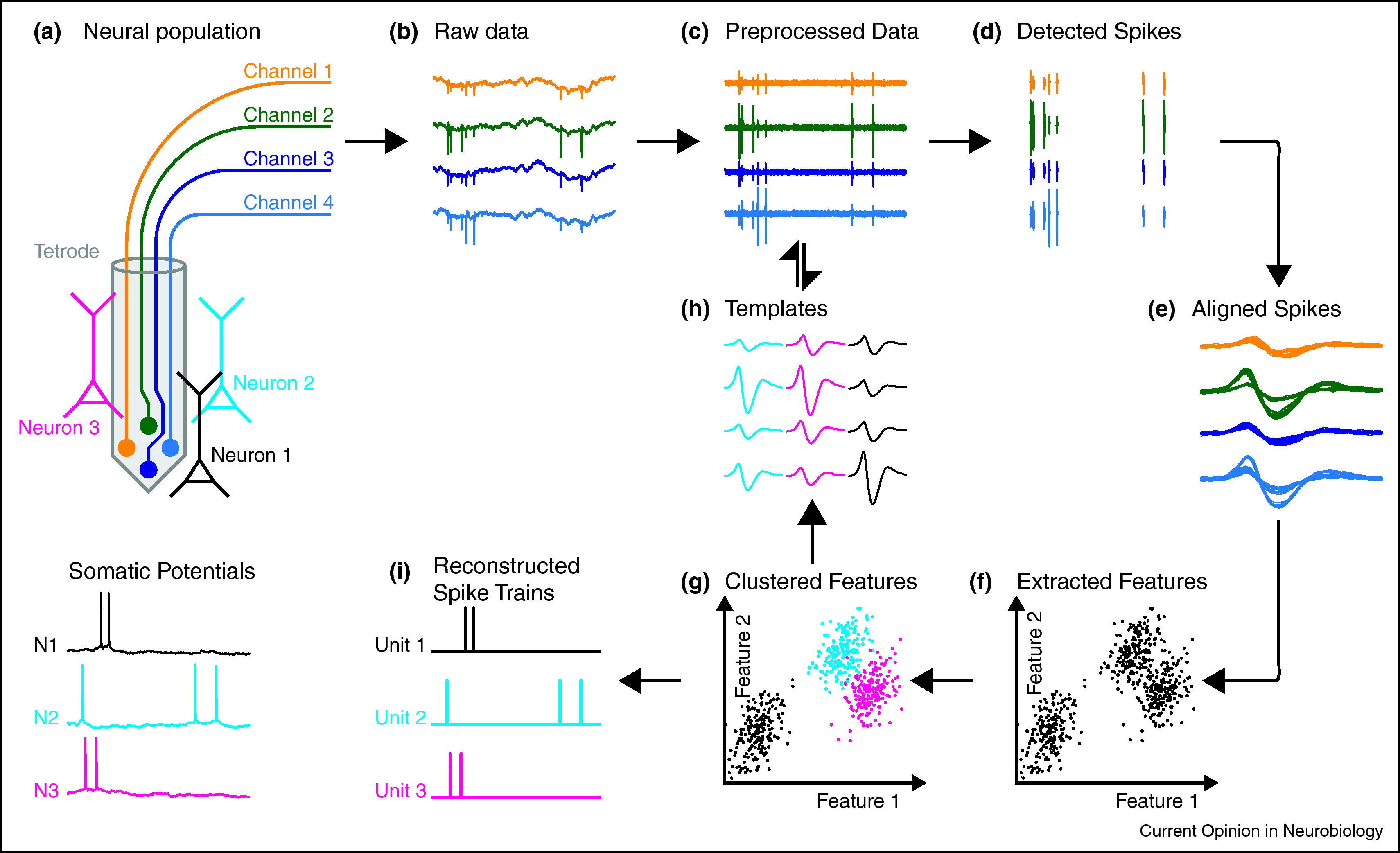
../_images/Einevoll2012.jpg

Fig. 7 An overview of the spike sorting problem and a solution based on clustering. Figure credit: Einevoll et al. [2012].#

With that background, we come to our first neural data analysis problem: spike sorting. The figure above illustrates the spike sorting problem. Electrophysiological recording devices like tetrodes (panel a) and Neuropixels probes (which we will discuss in the next chapter) provide measurements of the electric field in the vicinity of neurons. When those neurons spike, they cause a deflection in the voltage measured on the individual electrodes or channels of the device. The magnitude of the deflection depends on how far the neuron is from the recording site.

Problem Statement

The spike sorting problem is to identify the spikes in the multi-channel voltage recording and assign those spikes to individual neurons based on the spike waveform and the channels that were activated.

In the next few chapters, we will develop increasingly sophisticated solutions to this problem. We’ll start by framing the problem as a clustering problem in machine learning, but as we will see, this formulation has a few key limitations. In the next chapters, we will frame the problem as a matrix factorization problem, and then as a convolutional matrix factorization problem. Each step will improve on the previous, leading to a model and algorithm that is close to the state-of-the-art approaches to this fundamental problem in neural data analysis.

Breaking down the problem#

Let’s start simple. One way to approach this problem is to break it down into a few steps.

  1. Preprocessing the data to remove artifacts and slow fluctuations.

  2. Detect spikes in the preprocessed voltage trace.

  3. [Optionally] Extract features of the spike waveforms

  4. Infer which neuron produced each spike.

Preprocessing#

Before we go looking for spikes, we need to take care of a few preprocessing steps to obtain a nice trace like what you see in panel c above.

Bandpass filtering#

Raw voltage traces exhibit large, slow fluctuations over time called the local field potential (LFP) [Einevoll et al., 2013]. The LFP is typically defined as the low frequency part of the signal, up to 300-500Hz. Extracellular action potentials (EAPs) or spikes, by contrast, are fast deflections in the voltage, with frequencies in the range of 300-3000Hz. Since we are looking for those spikes, a common first step is to bandpass filter the raw voltage traces using, for example, a Butterworth filter.

Whitening the signal#

Another challenge arises from correlated noise across channels. A common next step of preprocessing is to whiten the data. Let \(\mbY \in \reals^{T \times N}\) denote the bandpass filtered signal. It is \(T\) samples long and \(N\) channels wide. Electrophysiological voltage traces are recorded with high sampling frequencies, around 30 kHz, so a 1 minute long recording would have \(T=60 \times 30 \times 10^3 = 1.8 \times 10^6\) samples.

The bandpass filter effectively removes the zero-frequency component of the raw signal — i.e., the mean — So each column of \(\mbY\) should be mean zero. Thus, the empirical covariance across channels is given by,

\[\begin{align*} \hat{\mbSigma} &= \frac{1}{T} \sum_{t=1}^T (\mby_t - \bar{\mby}) (\mby_t - \bar{\mby})^\top \\ &= \frac{1}{T} \sum_{t=1}^T \mby_t \mby_t^\top \\ &= \frac{1}{T} \mbY^\top \mbY. \end{align*}\]

To whiten the signal, we need to multiply an inverse square root of the covariance matrix. The eigendecomposition of the covariance matrix is given by \(\hat{\mbSigma} = \mbV \mbLambda \mbV^{-1}\), where \(\mbV\) is a matrix of eigenvectors and \(\mbLambda = \diag(\lambda_1, \ldots, \lambda_N)\) is a diagonal matrix of eigenvalues.

Eigendecomposition of covariance matrices

Since \(\hat{\mbSigma}\) is a covariance matrix, it must be positive semi-definite (PSD). The eigendecomposition of a PSD has a few nice properties:

  1. The eigenvalues are real-valued and non-negative (\(\lambda_n \in \reals_+\))

  2. The eigenvectors are real-valued and orthogonal to one another, so \(\mbv_n^\top \mbv_{n'} = 1\) if \(n=n'\) and 0 otherwise.

Moreover, since the eigenvectors are orthogonal, the inverse of \(\mbV\) is simply the transpose, \(\mbV^{-1} = \mbV^\top\).

To obtain an inverse square root of the covariance matrix, we can simply take the inverse square root of the eigenvalues,

\[\begin{align*} \hat{\mbSigma}^{-\frac{1}{2}} &= \mbV \mbLambda^{-\frac{1}{2}} \mbV^{-1} = \mbV \mbLambda^{-\frac{1}{2}} \mbV^{\top}, \end{align*}\]

where the second equality follows from the fact that the eigenvectors are orthogonal (see box above).

Finally, the whitened signal is

\[\begin{align*} \mbY^{(\mathsf{w})} &= \mbY \hat{\mbSigma}^{-\frac{1}{2}}. \end{align*}\]

It is easy to check that the whitened signal has identity covariance.

Proof

Since the whitened signal is also mean zero, its covariance is given by,

\[\begin{align*} \frac{1}{T} (\mbY^{(\mathsf{w})})^\top \mbY^{(\mathsf{w})} &= \frac{1}{T} (\mbY \hat{\mbSigma}^{-\frac{1}{2}})^\top (\mbY \hat{\mbSigma}^{-\frac{1}{2}}) \\ &= (\hat{\mbSigma}^{-\frac{1}{2}})^\top (\frac{1}{T} \mbY^\top \mbY) \hat{\mbSigma}^{-\frac{1}{2}} \\ &= (\hat{\mbSigma}^{-\frac{1}{2}})^\top \hat{\mbSigma} \hat{\mbSigma}^{-\frac{1}{2}} \\ &= \mbV \mbLambda^{-\frac{1}{2}} \mbV^\top \mbV \mbLambda \mbV^\top \mbV \mbLambda^{-\frac{1}{2}} \mbV^\top \\ &= \mbV \mbLambda^{-\frac{1}{2}} \mbLambda \mbLambda^{-\frac{1}{2}} \mbV^\top \\ &= \mbI. \end{align*}\]

Note

Note that the whitening transformation will typically rotate the signal so that columns of \(\mbY^{(\mathsf{w})}\) no longer correspond to individual channels, but rather to linear combinations of the original channels. This is in contrast to simply z-scoring each channel separately, which would ensure that each channel is mean zero and unit variance, but would not guarantee that they are uncorrelated. We will still refer to the columns of the whitened signal as “channels” in the sections below, but it is important to keep this caveat in mind.

After bandpass filtering and whitening, we’re ready to start spike sorting!

Detecting spikes#

The next step of the process is to infer spike times by looking for pronounced dips in the signal on at least one channel. Recall from the previous chapter than extracellular action potentials typically produce negative spikes, so we are looking for dips in the traces.

To stand out from the noise, a spike should be about 4 standard deviations below the mean. After whitening, each channel has unit variance, so we are looking for dips of at least -4 in magnitude on at least one channel.

If we simply thresholded the traces, we would find that the signal dips below -4 for many samples in a row. We just want to find the trough of this signal — i.e., the most negative point. To that end, we typically impose a constraint on the distance between detected spike times. For example, we might require that detected spikes be separated by at least 3 ms. At a sampling frequency of 30 kHz, that constraint would require detected spikes to be separated by at least 90 samples.

The scipy.signal.find_peaks is useful for this task, and we will make use of it in the lab.

Finally, once we have identified the spike times, we will extract a window around each spike. We call these windows the spike waveforms. Formally, let \(\{t_s\}_{s=1}^S\) denote the detected spike times. Each \(t_s\) is a number in the range \(\{1,\ldots, T\}\). For each spike, we will extract a window of length \(D\), centered on the spike time.

Let \(\mbX_s \in \reals^{D \times N}\) denote the window around the \(t\)-th spike. Using Python notation for slicing, we say,

\[\begin{align*} \mbX_s = \mbY^{(\mathsf{w})}_{t_s - \frac{D}{2}:t_s + \frac{D}{2}}. \end{align*}\]

The full set of spike waveforms combines into the 3D tensor \(\mbX = \{\mbX_s\}_{s=1}^S \in \reals^{S \times D \times N}\) with individual entries denoted by \(x_{s,d,n}\)

Clustering spikes#

Now that we have detected spikes and extracted their corresponding waveforms, the next step is to infer which neuron caused each spike. The key idea is that each neuron will produce a characteristic waveform across the \(N\) channels, which depends on the biophysical properties of the cell and how close it is to each channel. Our goal is to sort the spike waveforms into different groups based on their shapes, so that each group corresponds to a different neuron.

From a machine learning standpoint, this is a clustering problem. One way to solve such problems is using mixture models. Mixture models are probabilistic models that make specific assumptions about how the spike waveforms arise, as we discus below.

Modeling assumptions#

We make a few basic assumptions that can be codified in a probabilistic mixture model.

  1. Assume there are \(K\) neurons in the vicinity of the probe. When the \(k\)-th neuron spikes, its EAP produces a signature template on the channels. The template is a matrix, \(\mbW_k \in \reals^{D \times N}\), with entries \(w_{k,d,n}\) representing the average magnitude of the EAP produced on channel \(n\) at time lag \(d\) each time neuron \(k\) spikes.

  2. The voltage recordings are noisy. The observed spike waveforms match the template of the neuron that caused the spike, but they are corrupted by independent, additive Gaussian noise \(\epsilon_{s,d,n} \in \mathcal{N}(0, \sigma^2)\) for each channel \(n\), time lag \(d\), and spike \(s\).

  3. Each spike waveform \(\mbX_s\) can be attributed to exactly one neuron, denoted by the variable \(z_s \in \{1,\ldots,K\}\). This assumption essentially says that it is unlikely for two neurons to spike in the same window of time if \(D\) is small. However, as we will see in the following chapters, this assumption may not be warranted!

The Gaussian distribution#

To formalize this probabilistic model, we need to introduce the Gaussian distribution.

The Gaussian Distribution

We denote a Gaussian (aka normal) random variable \(x \in \mathbb{R}\) by,

\[ x \sim \cN(\mu, \sigma^2), \]

where \(\mu = \mathbb{E}[x]\) is the mean and \(\sigma^2 = \mathbb{V}[x]\) is the variance. The Gaussian pdf is,

\[ \cN(x; \mu, \sigma^2) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left\{ -\frac{1}{2 \sigma^2}(x - \mu)^2\right\}. \]

The Gaussian distribution has many important properties. For example,linear transformations of \(x\) are also Gaussian:

\[ x \sim \cN(\mu, \sigma^2) \Rightarrow ax + b \sim \cN(a \mu + b, a^2 \sigma^2). \]

We will cover more nice properties of the Gaussian distribution as the course goes on.

The Likelihood#

With these facts, our assumptions above correspond to a Gaussian likelihood for the spike waveforms given the neuron assignments,

\[\begin{align*} p(\mbX_s \mid z_s = k) &= \prod_{d=1}^D \prod_{n=1}^N \cN(w_{k,d,n}, \sigma^2). \end{align*}\]

The product over time lags \(d\) and channels \(n\) is due to the independence assumptions we made about the noise.

Prior distribution on spike assignments#

We also need to specify the probability of different spike assignments, \(z_s \in \{1,\ldots,K\}\). Since the spike assignments take one of \(K\) discrete values, we can model them as draws from a categorical distribution,

\[\begin{align*} z_s &\sim \mathrm{Cat}(\mbpi), \end{align*}\]

where \(\mbpi = (\pi_1, \ldots, \pi_K)\) is a vector of prior probabilities for each neuron. We have \(\pi_k \geq 0\) for all \(k\), and \(\sum_k \pi_k = 1\).

In other words, \(\mbpi\) is a length-\(K\) vector in the probability simplex, which we denote by \(\mbpi \in \Delta_{K-1}\).

Prior distribution on templates and neuron probabilities#

Finally, we could complete the model with a prior distribution on the templates, \(\mbW\). For example, we could constrain the magnitude of the templates, or even limit their rank (since they are matrices). For now, we will keep it simple and forgo a prior on templates, but we will revisit these ideas in the next chapters.

Likewise, we could put a prior on the neuron proabilities, \(\mbpi\). In this case, the Dirichlet distribution is a conjugate prior. Again, we will forgo that level of detail for now.

Improper priors

If we really want to be Bayesian about our model, we need a prior of \(\mbW\). However, the weakest prior is to say all templates are equally likely,

\[\begin{align*} p(\mbW_k) \propto 1. \end{align*}\]

Since \(\mbW_k\) is a real-valued matrix, this is an improper prior: the density does not integrate to one. Improper priors can cause technical headaches for Bayesian analyses, but since we will just be making point estimates of the model parameters, it won’t hurt us in this setting.

In other words, you can either treat the templates as model parameters (without priors) or as latent variables (with improper uniform priors), and the algorithms below remain the same.

The joint probability#

Finally, we can write the joint probability of the spike waveforms \(\mbX = \{\mbX_s\}_{s=1}^S\) and spike assignments \(\mbz = \{z_s\}_{s=1}^S\) under the templates \(\mbW = \{\mbW_k\}_{k=1}^K\) as follows,

\[\begin{align*} p(\mbX, \mbz; \mbW, \mbpi) &= \prod_{s=1}^S p(\mbX_s \mid z_s; \mbW) \, p(z_s; \mbpi) \\ &= \prod_{s=1}^S \left[\prod_{d=1}^D \prod_{n=1}^N \cN (x_{s,d,n} \mid w_{z_s,d,n}, \sigma^2 ) \right] \mathrm{Cat}(z_s; \mbpi) \end{align*}\]

(We suppressed the dependence on the variance \(\sigma^2\) since we will treat it as a fixed hyperparameter for now.)

Fitting the model#

Like last time, we will “fit” the model by performing maximum a posteriori (MAP) estimation with coordinate ascent. Specifically, our algorithm will be:

  • repeat until convergence:

    • compute the log joint probability under the current parameters, \(\log p(\mbX, \mbz; \mbW, \mbpi)\).

    • for \(s=1,\ldots,S\):

      • Set \(z_s = \arg \max_k \; p(\mbX_s \mid z_s=k) \, p(z_s=k)\) holding \(\mbW\) and \(\mbpi\) fixed

    • for \(k=1,\ldots,K\):

      • Set \(\mbW_k = \arg \max \; p(\mbX, \mbz; \mbW, \mbpi)\) holding \(\mbz\) and \(\mbpi\) fixed

    • set \(\mbpi = \arg \max \; p(\mbX, \mbz; \mbW, \mbpi)\) holding \(\mbz\) and \(\mbW\) fixed

The log joint probability should go up each iteration since each update maximizes it with respect to one variable. We will track this quantity to monitor convergence.

Updating the assignments#

To update the spike assignments, we need to maximize the joint probability as a function of \(z_s\), holding everything else fixed. Maximizing the joint probability wrt \(z_s\) is equivalent to maximizing the log joint probability, since the logarithm is a monotonically increasing function. Moreover, since \(z_s\) only appears in a few terms in the log joint probability, the objective simplifies to,

\[\begin{align*} \cL(z_s) &= \log p(\mbX_s \mid z_s=k) + \log p(z_s=k) + \mathrm{const}\\ &= \left[\sum_{d=1}^D \sum_{n=1}^N \log \cN(x_{s,d,n} \mid w_{z_s,d,n}, \sigma^2) \right] + \log \mathrm{Cat}(z_s; \mbpi) + \mathrm{const} \end{align*}\]

Substituting the definition of the Gaussian pdf and the categorical pmf,

\[\begin{align*} \cL(z_s) &= \left[\sum_{d=1}^D \sum_{n=1}^N -\frac{1}{2\sigma^2} (x_{s,d,n} - w_{z_s,d,n})^2 \right] + \log \pi_{z_s} + \mathrm{const} \end{align*}\]

Since \(z_s\) can only take on \(K\) values, we can simply evaluate this objective for each setting of \(z_s\) and choose the one with the largest log probability.

Updating the waveforms#

Now consider optimizing the waveforms. Maximizing the joint probability wrt \(\mathbf{W}_k\) is equivalent to maximizing the log joint probability, which is

\[\begin{align*} \cL(\mbW_k) &= \log p(\mbX, \mbz; \mbW, \mbpi) \\ &= \sum_{s=1}^S \sum_{d=1}^D \sum_{n=1}^N \log \mathcal{N}\left(x_{s,d,n} \mid w_{z_s,d,n}, \sigma^2 \right) + \mathrm{const} \\ &= \sum_{s: z_s=k} \sum_{d=1}^D \sum_{n=1}^N \log \mathcal{N}\left(x_{s,d,n} \mid w_{k,d,n}, \sigma^2 \right) + \mathrm{const} \\ \end{align*}\]

where in the second line we isolated just the spikes currently assigned to neuron \(k\).

This objective separates into a sum over the entries of \(\mbW_k\). We can optimize each entry independently. With a bit of calculus, it’s easy to show that the optimum is obtained at,

\[\begin{align*} w_{k,d,n} &= \frac{1}{S_k} \sum_{s:z_s=k} x_{s,d,n} \end{align*}\]

where \(S_k = \sum_s \bbI[z_s=k]\) is the number of spikes assigned to neuron \(k\).

Optimizing the neuron probabilities#

Optimizing the neuron probabilities is a bit more involved since \(\mbpi\) is constrained to the probability simplex, but with a bit of calculus you can show that the log joint probability as a function of \(\mbpi\) is maximized at,

\[\begin{align*} \pi_k &= \frac{S_k}{S}. \end{align*}\]

Tracking convergence#

Each step of the algorithm should increase the log joint probability, ultimately leading us to a local optimum of this objective funciton. To monitor convergence, we compute the log joint probability after each iteration, and when it stops increasing we halt.

Other considerations#

There are several other considerations to keep in mind, and we discuss a few of them here.

  1. Inferring the number of neurons, \(K\). We don’t know how many neurons could be contributing to the spike waveforms! This isn’t just a problem with spike sorting — it’s generally a hard problem with clustering. One common approach is to hold out a subset of the data (in our case, a subset of the spike waveforms \(\mbX_s\)) and evaluate the log probability of the held-out data using the parameters fitted on the training data. for example, once we have estimated the parameters \(\mbW\) and \(\mbpi\) on the training data, we can evaluate the likelihood of a held-out waveform \(\mbX_s\) by first finding the most likely assignment \(z_s\) and then evaluating \(\log p(\mbX_s \mid z_s; \mbW)\). Alternatively, we could evaluate the marginal log probability of the held-out waveform, \(\log p(\mbX_s; \mbW, \mbpi) = \log \sum_k p(\mbX_s \mid z_s=k; \mbW) p(z_s=k; \mbpi)\).

  2. Lack of ground truth. How do we know if we’re right? Spike sorting is an unsupervised learning problem, so we generally don’t have ground truth! However, we can simulate realistic voltage traces from a biophysical model with known, ground truth spikes and assignments. Then we can evaluate how well our procedure recovers the ground truth. We will take this approach in the labs.

  3. Misspecified modeling assumptions. The assumptions above could be wrong in many ways. Spikes from a given neuron may not always follow the same template. The noise may not be Gaussian. Several neurons could spike at once, leading to superimposed waveforms. Probabilistic modeling always requires us to make assumptions, and there are always trade-offs involved. We have specified a few simple and reasonable assumptions, but lots of research has gone into improving and relaxing these assumptions.

  4. Estimating high-dimensional parameters with limited data. The approach developed above requires us to estimate the templates \(\mbW_k\) for each neuron. Those templates are matrices of size \(D \times C\), and typically they will have hundreds of entries (free parameters). If we don’t observe many spikes from a given neuron, then it could be hard to estimate all these parameters reliably. In practice, most spike sorting algorithms make assumptions to combat this issue. For example, we could use off-the-shelf dimensionality reduction methods like principal components analysis (PCA) to project the spike waveforms into a lower-dimensional feature space before clustering. Alternatively, we could constrain the templates to be low rank, so that the number of free parameters scales as \(\cO(D+C)\) rather than \(\cO(DC)\). For simplicitly, we omitted these details, but we will revisit them in the next chapter.

Conclusion#

This chapter introduced the spike sorting problem for electrophysiological (“ephys”) recordings.
The algorithm we described here is not that far from MountainSort [Chung et al., 2017] and otherwidely used spike sorting algorithms [], e.g.. These approaches often involved more sophisticated techniques to relax the Gaussian assumptions of the model above. However, with the advent of silicon probes like NeuroPixels, which have dozens of densely packed channels, different approaches are needed. We will discuss these next.

Contents